|
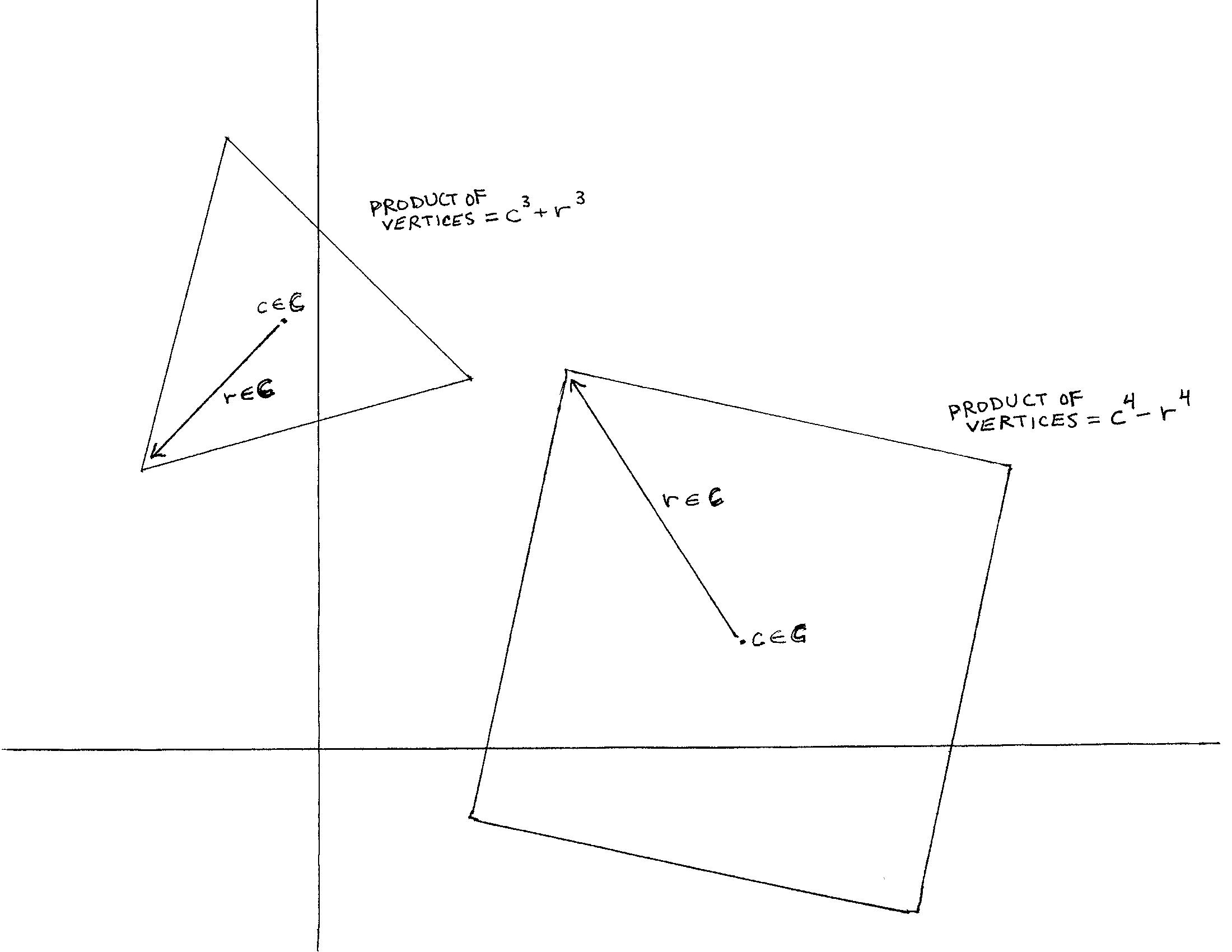
^ I discovered this theorem sometime in the winter of 2023-2024 (northern hemisphere) while working on some other mathematical ideas, when, in the middle of the night, while listening to my favorite medley of various versions of the best song ever written (Pachelbel's Canon: https://www.youtube.com/watch?v=Sxcc3YSrCs8), I very earnestly prayed to Yahweh/God and asked Him to give me *some* worthwhile result out of the mass of ideas I was contemplating at the time, for His glory. I immediately began drawing a large, generalized square (in terms of its center and a complex radius) on a piece of graph paper (complex plane), and then decided for no particular reason to multiply its vertices. Seeing the result, I then did the same for a generalized equilateral triangle. From here, the conjecture was somewhat easy to suspect (though the +/- for odd/even \(n\)-gons threw me off at first), but it seemed too good to be true. "Coincidentally" at the same time I also had open on my computer screen the wikipedia entry for Vieta's Formulas, which I had never looked at before that night (even though I've gone through 3 years of an undergrad math degree — I now believe that every math undergrad should be given some instruction on Vieta's formulas.) Well, the proof jumped out in my mind, and everything came together within about 10 minutes of my prayer. I cried.
For the next few months, I tried to use the theorem as part of a larger, seemingly unrelated theory I'm working on, but that hasn't clicked yet. (And, yes, it does beg to be used in attempts at a proof of Fermat-Wiles, elementary or otherwise; I gave it a go, but didn't get anywhere with it. Maybe you will see a way.)
Recently I decided it was time to share this with others. When I presented the statement of this theorem to a college professor, he said it's "just a computation", and that mathematicians wouldn't find it very interesting. But that characterization is wrong.
The reality is that this neat little theorem is not mere "computation", but actually a quite elegant result which demonstrates a beautiful geometric property of the complex numbers which is apparently little-known (why would that be the case?) or unknown (which is almost unimaginable). Either way, I think this gem should be in every introductory text on the complex numbers, either as an example, or as an excercise. What do you think? Comment below.
— Lance Horner (May 21, 2024)
contact: lancehorner.montgomerycollege@gmail.com ← I'm not affiliated with that college (or any other institution); it's just an old email I use for now.
|